En este artículo, exploramos el análisis detallado de un circuito eléctrico que incorpora seis resistencias y dos fuentes de voltaje, utilizando las Leyes de Kirchhoff para determinar el flujo de corriente y la potencia disipada en cada componente. Este procedimiento es fundamental en la ingeniería eléctrica para comprender el comportamiento de los circuitos y optimizar su diseño.
Descripción del Circuito
El circuito analizado incluye las siguientes características:
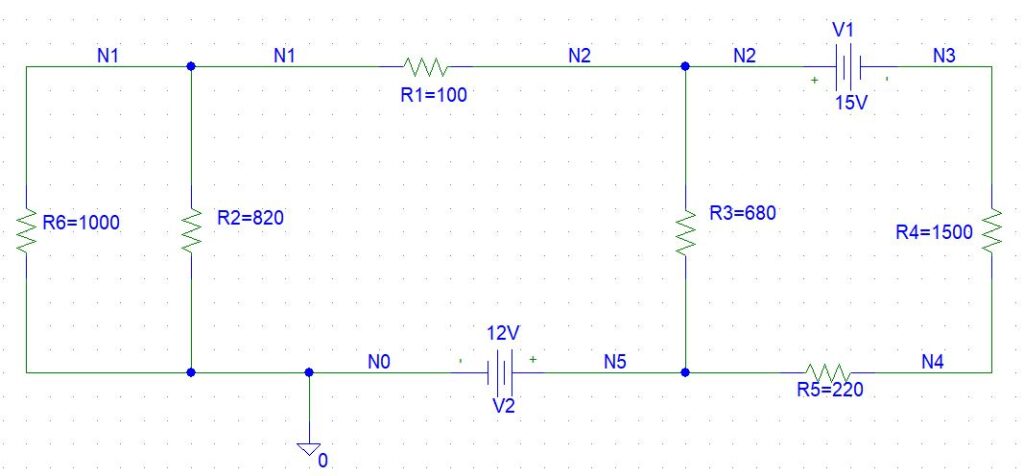
- Seis resistencias con valores de R1=100Ω, R2=820Ω, R3=680Ω, R4=1500Ω, R5=220Ω, y R6=1000Ω.
- Dos fuentes de voltaje: una de 12V entre los nodos N0 y N5, y otra de 15V entre N2 y N3.
- Configuración de resistencias:
- R2 y R6 en paralelo entre N0 y N1.
- R1 conecta N1 y N2.
- R3 se sitúa entre N2 y N5.
- R4 y R5 forman una serie entre N3, N4, y N5.
Metodología de Análisis por Leyes de Kirchhoff
El análisis se basa en las Leyes de Kirchhoff:
- Ley de Voltaje de Kirchhoff (LVK): La suma de todas las caídas de voltaje en un lazo cerrado es igual a la suma de todas las fuentes de voltaje en ese lazo.
- Ley de Corriente de Kirchhoff (LCK): La suma de las corrientes que entran a un nodo es igual a la suma de las corrientes que salen de ese nodo.
Ecuaciones Utilizadas
Para resolver el circuito, aplicamos LVK y LCK y formulamos las siguientes ecuaciones principales:
Para el lazo que incluye las resistencias en paralelo (R2 y R6) y la resistencia R1:
I1 * (R2 + R6) - I2 * R2 = 0
Para el lazo que incluye R1, R2, R3, y la fuente de 12V:
-I1 * R2 + I2 * (R2 + R1 + R3) - I3 * R3 = 12
Para el lazo que incluye R3, R4, R5, y la fuente de 15V:
-I2 * R3 + I3 * (R3 + R5 + R4) = 15
Resultados y Discusión
Resolviendo las ecuaciones, determinamos las corrientes en cada resistor y calculamos la potencia disipada usando P = I^2 * R. La tabla final con los resultados es:
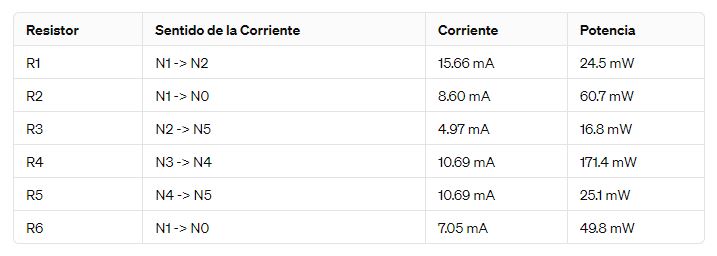
Esta tabla muestra el sentido de la corriente para cada resistor dentro del circuito, junto con los valores de corriente que fluyen a través de ellos y la potencia que cada uno disipa, basado en los cálculos previos.