Introducción:
En el ámbito de la ingeniería eléctrica, las transformaciones de estrella (Y) a delta (Δ) y de delta a estrella son técnicas fundamentales para simplificar el análisis de circuitos complejos que contienen arreglos de resistencias. Estos métodos no solo facilitan la resolución de redes complicadas, sino que también son cruciales para el diseño y análisis de sistemas de potencia, circuitos electrónicos y redes de telecomunicaciones. Este artículo habla de forma simple el cómo y el porqué de estas transformaciones, ofreciendo a los lectores una comprensión del concepto y aplicaciones prácticas de estas técnicas esenciales.
Conceptos Básicos:
Antes de adentrarnos en las transformaciones propiamente dichas, es vital entender los arreglos de estrella y delta en el contexto de los circuitos eléctricos. Un arreglo en estrella conecta tres resistencias (o impedancias en circuitos AC) desde un punto común, formando la figura de una «Y». Por otro lado, un arreglo delta conecta tres resistencias en forma de triángulo o delta (Δ), sin un punto central común.
Transformación de Estrella a Delta:
La transformación de estrella a delta permite a los ingenieros convertir un arreglo de resistencias conectadas en una configuración de estrella en una configuración delta equivalente. Esta conversión es vital en situaciones donde los análisis de circuitos requieren una forma específica para simplificar el proceso de cálculo.
Las ecuaciones para convertir resistencias en una configuración de estrella a una configuración delta son las siguientes:��=�1⋅�2+�2⋅�3+�
R_{Δ1} = \frac{R_{Y1} \cdot R_{Y2} + R_{Y2} \cdot R_{Y3} + R_{Y3} \cdot R_{Y1}}{R_{Y2}}R_{Δ2} = \frac{R_{Y1} \cdot R_{Y2} + R_{Y2} \cdot R_{Y3} + R_{Y3} \cdot R_{Y1}}{R_{Y3}}R_{Δ3} = \frac{R_{Y1} \cdot R_{Y2} + R_{Y2} \cdot R_{Y3} + R_{Y3} \cdot R_{Y1}}{R_{Y1}}En la figura adjunta se muestra cómo luce el circuito antes y despues de la transformación. Las ecuaciones funcionan en los dos sentidos. de (Δ) a Y y de (Y) a (Δ).
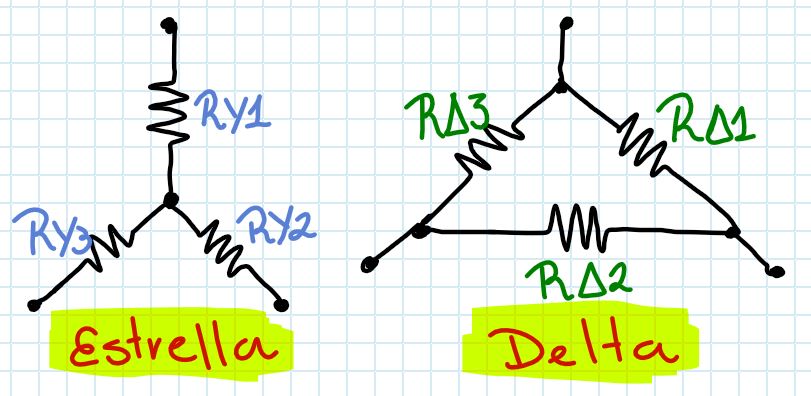
Transformación de Delta a Estrella:
Inversamente, la transformación de delta a estrella facilita la conversión de una configuración delta de resistencias a una configuración de estrella equivalente. Esta técnica es igualmente importante cuando se analizan circuitos en los que una configuración de estrella simplifica la resolución de corrientes y tensiones.
Las fórmulas para esta transformación son:
R_{Y1} = \frac{R_{Δ1} \cdot R_{Δ3}}{R_{Δ1} + R_{Δ2} + R_{Δ3}}R_{Y2} = \frac{R_{Δ1} \cdot R_{Δ2}}{R_{Δ1} + R_{Δ2} + R_{Δ3}}R_{Y3} = \frac{R_{Δ2} \cdot R_{Δ3}}{R_{Δ1} + R_{Δ2} + R_{Δ3}}�1=��⋅����+Aplicaciones Prácticas: Estas transformaciones son herramientas poderosas para el análisis de circuitos, especialmente en situaciones donde directamente medir las resistencias no es posible o práctico. Se aplican en el diseño de filtros, la adaptación de impedancias, y en el análisis de circuitos balanceados y desbalanceados en sistemas de potencia.
Conclusión:
Entender y aplicar las transformaciones de estrella a delta y viceversa es esencial para cualquier ingeniero eléctrico. Estas técnicas no solo simplifican el análisis de circuitos complejos, sino que también abren la puerta a una comprensión más profunda de la teoría de circuitos y sus aplicaciones prácticas.
Referencias:
- W.H. Hayt, J.E. Kemmerly, y S.M. Durbin, «Análisis de Circuitos en Ingeniería», 8va Edición, McGraw-Hill, 2012.
- A. Bruce Carlson, «Circuitos: Análisis y Diseño», 3ra Edición, Cengage Learning, 2007.
Estas referencias proporcionan una base sólida para una exploración más profunda del tema y son accesibles para aquellos que buscan ampliar su comprensión de las transformaciones de estrella a delta y viceversa.