Modelo Dinámico de un Motor de DC en Laplace
El modelo de un motor de DC se divide en dos partes principales, la eléctrica y la mecánica, que están acopladas entre sí.
1. Parte Eléctrica
La parte eléctrica describe la dinámica de la corriente de armadura \(i_a(t)\) en función del voltaje de entrada \(v_a(t)\). Se modela como un circuito R-L con una fuerza contra-electromotriz \(e_a(t)\).
Ecuación diferencial: \(v_a(t)=R_ai_a(t)+L_a\frac{di_a(t)}{d_t}+e_a(t) \) Donde:
- \(v_a\): Voltaje de armadura
- \(i_a\): Corriente de armadura
- \(R_a\): Resistencia de armadura
- \(L_a\): Inductancia de armadura
- \(e_a\): Fuerza contra-electromotriz (se opone al flujo de corriente, es proporcional a la velocidad del motor: \(e_a(t)=K\Phi\omega(t)\)
Ecuación en Laplace: Tomando la transformada de Laplace (con condiciones iniciales cero): \(V_a(s)=R_aI_a(s)+sL_aI_a(s)+E_a(s) \). Agrupando: \(V_a(s)=(sL_a+R_a)I_a(s)+K\Phi\omega(s)\)
2. Parte Mecánica
La parte mecánica relaciona el torque desarrollado por el motor con la velocidad angular (ω) y las fuerzas de inercia y fricción.
Ecuación diferencial: \(T_m(𝑡) =J\frac{d\omega(t)}{dt}+K_{rot}\omega(t)+T_L(t)\) Donde:
- \(T_m\): Torque desarrollado por el motor (es proporcional a la corriente de armadura: \(T_m(t)=K\Phi i_a(t)\)
- \(J\): Inercia del rotor y de la carga
- \(K_{rot}\): Coeficiente de fricción viscosa
- \(\omega\): Velocidad angular
- \(T_L\): Torque de la carga
Ecuación en Laplace: \(T_m(s)=sJ\omega(s)+K_{rot}\omega(s)+T_L(s)\). Agrupando: \(K\Phi I_a(s)=(sJ+K_{rot})\omega(s)+T_L(s)\).
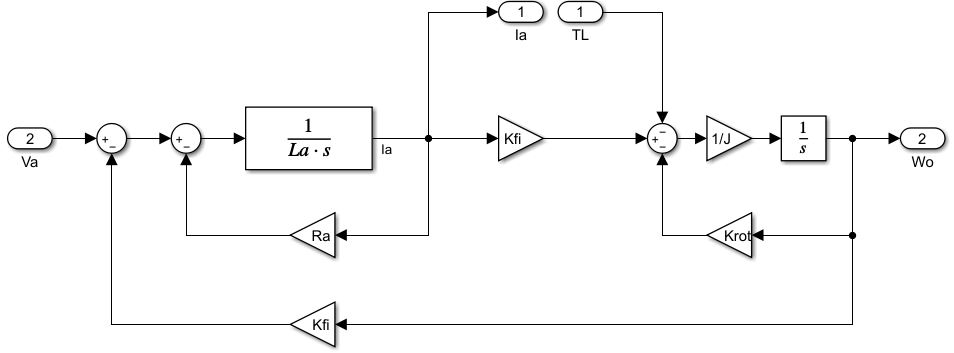
3. Modelo Completo en Diagrama de Bloques
Para visualizar la conexión entre ambas partes, podemos armar un diagrama de bloques completo del motor.
- La entrada es el voltaje de armadura \(V_a(s)\).
- La salida es la velocidad angular \(\omega(s)\).
- El acoplamiento se da por las constante \(K\Phi\). El torque \(T_m\) es proporcional a la corriente \(I_a\), y la fuerza contra-electromotriz \(E_a\) es proporcional a la velocidad \(\omega\).
Antes de ver las aplicaciones de los controladores PI para control de motores de DC, se realizará un repaso de lo que son sistemas de primer y segundo orden.
¿Qué es un Sistema de Primer Orden?
Un sistema de primer orden es aquel cuya dinámica puede describirse con una ecuación diferencial de primer orden. En la práctica, estos sistemas no tienen oscilaciones y su respuesta a un cambio de entrada es un crecimiento o decaimiento exponencial.
Son fundamentales porque muchos sistemas físicos se pueden modelar o aproximar con ellos, como:
- Un circuito RC o RL simple.
- El calentamiento de un cuerpo.
- La dinámica de la velocidad de un motor DC sin la inercia de la carga.
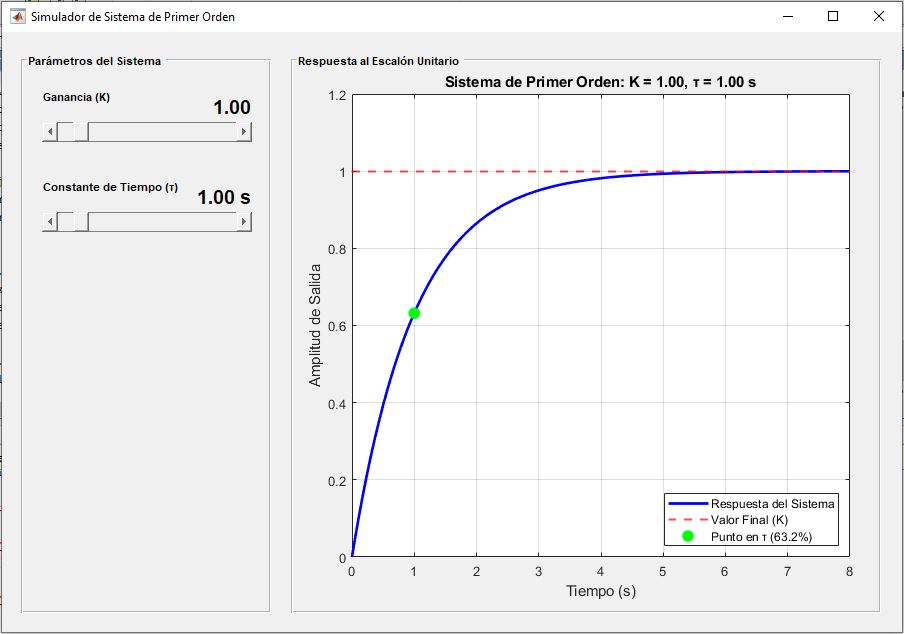
Ecuación Canónica y Parámetros Clave
La forma canónica de la función de transferencia de un sistema de primer orden en el dominio de Laplace es:
G(s)= U(s)Y(s) = \frac{K}{τs+1}
Donde:
- Y(s): Salida del sistema en el dominio de Laplace.
- U(s): Entrada del sistema en el dominio de Laplace.
- K (Ganancia Estática): Es el valor final (estado estable) de la salida del sistema cuando la entrada es un escalón unitario. Es decir,
K= \lim_{s \to 0} G(s)- τ (Constante de Tiempo): Este es el parámetro más importante. Define la velocidad de respuesta del sistema. Cuanto más pequeño sea τ, más rápido responderá el sistema a un cambio en la entrada. Físicamente, representa el tiempo que le toma a la salida alcanzar el 63.2% de su valor final después de una entrada de escalón.
Respuesta Típica al Escalón Unitario
Para una entrada de escalón unitario U(s)=1/s, la salida en el dominio del tiempo es:
y(t)=K(1−e^{−t/τ})La gráfica de esta respuesta es una curva exponencial suave que se aproxima al valor final de la ganancia K.
La constante de tiempo τ es muy útil para caracterizar la respuesta de un sistema:
- A t=τ, la respuesta ha alcanzado el 63.2% del valor final.
- A t=3τ, la respuesta está cerca del 95% del valor final.
- A t=4τ, la respuesta está en el 98% del valor final.
- A t=5τ, la respuesta se considera prácticamente en estado estable (más del 99% del valor final).
Entender la constante de tiempo es importante, ya que da una idea clara de la rapidez de un sistema. Al modelar la parte eléctrica o mecánica de un motor de DC, como se verá, estos sistemas de primer orden son la base para el lazo de control.
Descarga el siguiente fichero que corresponde a un script de Matlab, el cual fue escrito con aguda de Gemini de Google y manipula las constantes de tiempo y ganancia para comprender su funcionamiento. Debes cambiar la extensión .txt por .m y ejecutarlo como script desde la ventana inicial de matlab.
Sistemas de Segundo Orden: Ecuación Canónica
Un sistema de segundo orden es aquel cuya dinámica puede describirse con una ecuación diferencial de segundo orden. En el mundo del control, es una de las representaciones más importantes porque muchos sistemas físicos (como circuitos RLC, sistemas mecánicos con masa, resorte y amortiguador, y sí, ¡motores de DC!) pueden aproximarse o modelarse con este tipo de ecuación.
La ecuación canónica de un sistema de segundo orden en el dominio de Laplace es:
G(s)= \frac{Y(s)}{U(s)}= \frac{K\omega_n^2}{s^2 +2\zeta\omega_ns+\omega_n^2}\(\omega_n\) (Frecuencia Natural no Amortiguada): Representa la frecuencia a la que el sistema oscilaría si no tuviera amortiguamiento. Es un indicador de la velocidad de respuesta del sistema. Un omega_n más grande generalmente significa una respuesta más rápida. \(\omega_n\) se relaciona directamente con el tiempo de estabilización del sistema \(t_s\), es decir el tiempo que pasa del escalón hasta que llega a su valor final en una franja determinada. La relación entre estas variables se da por:
t_s=\frac{4}{\zeta \omega_n}\( \zeta \) (Factor de Amortiguamiento): Este es uno de los parámetros más importantes. Describe cómo las oscilaciones de la respuesta se van «amortiguando» con el tiempo. El valor de \( \zeta \) determina la naturaleza de la respuesta transitoria del sistema:
- \( \zeta > 1 \) (Sobreamortiguado):La respuesta es lenta y no oscila. El sistema se aproxima a su valor final sin sobrepasar.
- \( \zeta = 1 \) (Críticamente Amortiguado): Es la respuesta más rápida posible sin oscilar. El sistema alcanza su valor final en el menor tiempo posible sin sobrepaso.
- \(0 < \zeta < 1 \) (Subamortiguado): La respuesta es oscilatoria. El sistema sobrepasa su valor final y oscila antes de estabilizarse. Cuanto menor sea el valor de \( \zeta \), mayor será el sobrepico (el primer pico después de la entrada) y las oscilaciones.
- \( \zeta = 0 \) (No Amortiguado): La respuesta es puramente oscilatoria y no se detiene nunca.
\(K\) (Ganancia Estática): Es el valor final (estado estable) de la salida del sistema para una entrada de escalón unitario. Es decir, \( K=\lim_{s \to 0}G(s) \).
Para el control de un motor de DC, por ejemplo, estos parámetros nos ayudan a predecir cómo se comportará la velocidad del motor ante un cambio en el voltaje de entrada. Queremos una respuesta que sea rápida \(\omega_n\) grande pero sin oscilaciones excesivas \( \zeta \) óptimo, cercano a \(0.707\).
Descarga el siguiente fichero que corresponde a un script de Matlab, el cual fue escrito con aguda de Gemini de Google y manipula las constantes de tiempo y ganancia para comprender su funcionamiento. Cambiar la extensión .txt por .m y ejecutarlo como script desde la ventana inicial de matlab.

Controlador PI (Proporcional-Integral)
El controlador PI es uno de los más usados en la industria, especialmente para controlar variables de estado estable como la velocidad de un motor de DC. La función de transferencia de un controlador PI es:
C(s)=K_p + \frac{K_i}{s}
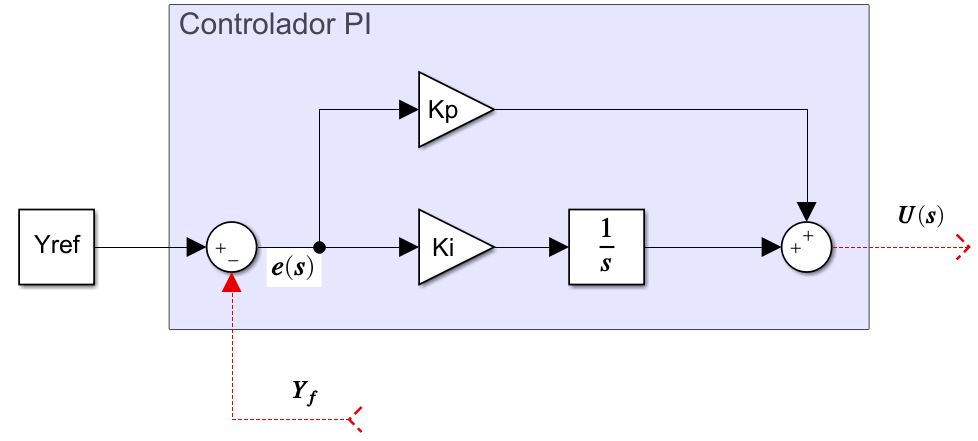
Acción Proporcional \((Kp)\): Actúa sobre el error actual del sistema. Si el error (la diferencia entre el valor deseado y el valor actual de la salida) es grande, el controlador genera una gran señal de control. Esto ayuda a que el sistema reaccione rápidamente a los cambios, pero un valor de \((Kp)\) muy alto puede causar inestabilidad y oscilaciones.
Acción Integral \( (\frac{K_i}{s}) \): Actúa sobre el error acumulado a lo largo del tiempo. Su principal función es eliminar el error en estado estable. Si el sistema se estabiliza con un pequeño error, la acción integral irá sumando este error hasta generar una señal de control que lo elimine por completo.
Se limitará la explicación del manejo del controlador PI para su aplicación en el control de motores de DC, donde la ecuación del controlador se procesa para que quede en una representación de un cero en el denominador y un polo en el origen:
- Función de Transferencia: La función de transferencia se reescribe de la siguiente manera:\(C(s)=K_p+\frac{K_i}{s}=K_p(1+\frac{K_i}{K_ps})=K_p(\frac{s+\frac{K_i}{K_p}}{s}) \). Si definimos la ganancia del controlador como \(K_c=K_p \) y la constante de tiempo integral como \( \tau_i=\frac{K_p}{K_i} \), la ecuación se convierte en: \(C(s)=K_c(\frac{1+\tau_is}{\tau_is})\)
¿Qué es el Control en Cascada?
El control en cascada es una arquitectura de control donde dos o más lazos de control se anidan o «encadenan» uno dentro del otro. Se caracteriza por tener un lazo de control interior y un lazo de control exterior.
- El lazo interior controla una variable que responde rápidamente, y su señal de salida es la entrada del lazo exterior. Este lazo se encarga de compensar las perturbaciones que afectan directamente a la variable interior.
- El lazo exterior controla una variable que responde más lentamente y genera la señal de referencia para el lazo interior.
La idea es simple: el lazo interior actúa como un «controlador esclavo» que ajusta una variable intermedia de forma rápida y precisa, mientras que el lazo exterior actúa como un «controlador maestro» que ajusta la variable principal del proceso, enviando la señal de referencia al lazo esclavo.
Ejemplo con Sistemas de Primer Orden y Controladores PI
Consideremos un sistema con dos procesos en serie, ambos modelados como funciones de transferencia de primer orden con ganancia unitaria:
- Proceso Interior \(G_1(s)\): Representa la dinámica más rápida, por ejemplo, el control de la corriente o par de un motor. \(G_1(s)=\frac{1}{\tau_1s+1} \)
- Proceso Exterior \(G_2(s)\): Representa la dinámica más lenta, por ejemplo, el control de la velocidad o posición del motor, que depende de la corriente. \(G_2(s)=\frac{1}{\tau_2s+1} \) Donde \(\tau_2 > > \tau_1 \).
Utilizaremos dos controladores PI, uno para cada lazo.
1. Lazo de Control Interior (Lazo Esclavo)
El primer paso es diseñar el lazo interior. Su objetivo es hacer que la variable interior (por ejemplo, la corriente) siga la referencia de forma rápida. Para ello, se usa un controlador PI, \( C_1(s)=(K_{p1}+\frac{K_{i1}}{s}) \), que retroalimenta la salida del proceso \(G_1(s)\).
- Sintonización: La sintonización del controlador \(C_1(s)\) es fundamental. Se diseña para que la respuesta de este lazo sea mucho más rápida que el lazo exterior. Esto se hace ajustando \(K_{p1}\) y \(K_{i1}\) para obtener una respuesta deseada (por ejemplo, críticamente amortiguada o subamortiguada con bajo sobrepico).
- Función del Lazo: Una vez sintonizado, el lazo interior (formado por \(C_1(s)\) y \(G_1(s)) \) se comporta como un nuevo «proceso» más rápido y estable. Las perturbaciones que afectan a \(G_1(s)\) son atenuadas de forma inmediata por este lazo.
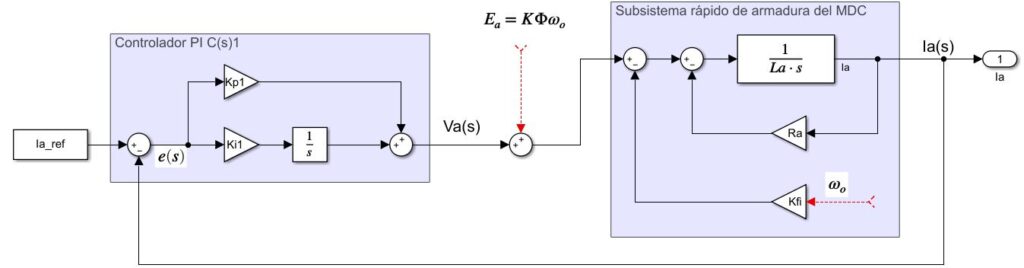
En la figura se muestra la unión entre el circuito de armadura de un MDC y el controlador PI interno de rápida respuesta. Note que el sistema de armadura se debe llevar a un sistema de primer orden, eso hace que la influencia de \(K\Phi\omega_o\) en la tensión de armadura se deba eliminar, eso se logra sumando esa misma cantidad a la salida del controlador, que será la tensión que se debe aplicar a la armadura \(V_a\) para generar una corriente igual a \(Ia_{ref}\) . A este proceso se le llama desacople de variables, y es super útil en el diseño de controladores en máquinas eléctricas, ya que son sistemas altamente acoplados.
2. Lazo de Control Exterior (Lazo Maestro)
El lazo exterior es el lazo principal. Su objetivo es controlar la variable más lenta (por ejemplo, la velocidad) utilizando un segundo controlador PI, \(C_2(s)=(K_{p2}+\frac{K_{i2}}{s})\). La señal de salida de este controlador es la referencia para el lazo interior.
- Sintonización: Al sintonizar \(C_2(s)\), se considera que el lazo interior ya sintonizado se comporta como una dinámica de primer orden o incluso una ganancia pura igual a 1, ya que es mucho más rápido. Esto simplifica enormemente la sintonización del lazo exterior.
- Función del Lazo: Este lazo se encarga de regular la variable principal. Por ejemplo, si la velocidad del motor es menor a la deseada, el controlador \(C_2(s)\) aumentará la referencia de corriente para el lazo interior, que a su vez hará que la corriente y, por ende, la velocidad aumenten.
En la siguiente figura se muestra la unión entre el sistema mecánico del MDC, el circuito de armadura con el controlador (que por su rápida respuesta se considera un sistema de ganancia unitaria) y el controlador PI del lazo exterior. Aqui, para llevar el sistema mecánico a un sistema de primer orden, se considera el par de carga \(T_L = 0\). El controlador del lazo exterior controlará la velcidad, y su salida será el par motor necesario para llevar al motor a la velocidad deseada. Aquí \(T_m\) se divide por \(K\Phi\) para encontrar la corriente \(Ia_{ref}\), que será la corriente que tiene que circular por la armadura.
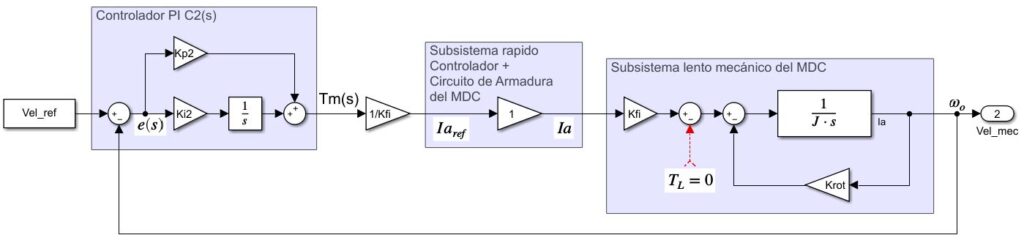
3. Ventajas del Control en Cascada
- Mejor Rechazo de Perturbaciones: Las perturbaciones que afectan al lazo interior son corregidas rápidamente por el controlador esclavo antes de que tengan un impacto significativo en la variable principal del lazo exterior.
- Sintonización Simplificada: El diseño se divide en pasos más sencillos. Primero se sintoniza el lazo rápido y luego el lazo lento.
- Mayor Estabilidad: Al controlar una variable intermedia, la estabilidad general del sistema mejora, permitiendo usar ganancias más altas en el controlador exterior sin causar inestabilidad.
- Respuesta Dinámica Mejorada: La velocidad y precisión en el seguimiento de la referencia aumentan, ya que el lazo interior puede corregir errores de forma casi instantánea.
En resumen, el control en cascada es una técnica poderosa que mejora la robustez y el rendimiento al dividir un problema de control complejo en lazos más pequeños y manejables, cada uno optimizado para una parte específica de la dinámica del sistema.
4. Calculo de Parámetros de los controladores en función de el tiempo de estabilización y amortiguamiento deseado.
Lazo de Control Interior: Dinámica de Corriente
Primero, nos enfocamos en el lazo de corriente, que es la parte más rápida.
- Proceso a controlar: La dinámica eléctrica del motor, representada por la función de transferencia: \(G_{eléctrico}(s)=\frac{I_a(s)}{V_a(s)}=\frac{1}{L_as+R_a}=\frac{1/R_a}{(L_a/R_a)s+1} \) Esta es una función de transferencia de primer orden con ganancia estática \(1/R_a\) y constante de tiempo \(\tau_e = L_a/R_a\).
- Controlador: Un controlador PI en forma paralela: \(C_1(s)=K_{p1}+\frac{K_{i1}}{s}=\frac{K_{p1}s+K_{i1}}{s}\)
- Lazo de Control: Al unir el controlador y el proceso en un lazo de retroalimentación unitaria, la función de transferencia de lazo cerrado es:
\frac{I_a(s)}{I_a{ref}(s)}=\frac{C_1(s)G_{eléctrico(s)}}{1+C_1(s)G_{eléctrico(s)}}.Sustituyendo las funciones de transferencia:
\frac{I_a(s)}{I_a{ref}(s)}=\frac{(\frac{K_{p1}s+K_{i1}}{s})(\frac{1}{L_as+R_a})}{1+(\frac{K_{p1}s+K_{i1}}{s})+(\frac{1}{L_as+R_a})}Simplificando tenemos qué:
\frac{I_a(s)}{I_a{ref}(s)}=\frac{K_{p1}s+K_{i1}}{s(L_as+R_a)+(K_{p1}s+K_{i1})}=\frac{K_{p1}s+K_{i1}}{L_as^2+(R_a+K_{p1})s+K_{i1}}El polinomio característico de este lazo es el denominador de la función de transferencia:
L_as^2+(R_a+K_{p1})s+K_{i1}Para sintonizar los parámetros \(K_{p1}\) y \(K_{i1}\), hacemos que este polinomio coincida con la forma canónica de un sistema de segundo orden que vimos en el repaso, \(s^2+2\zeta\omega_ns+\omega_n^2\). Dividiendo nuestro polinomio característico por \(L_a\) para que el coeficiente de \(s^2\) sea 1, obtenemos:
s^2 +\frac{R_a +K_{p1}}{L_a}s+\frac{K_{i1}}{L_a}La ecuación anterior es la más importante y la que usaremos para calcular las constantes del controlador en todos los ejercicios que se plantearán para diseño de los controladores de motores de DC.
Pasos:
Igualamos los coeficientes del polinomio caracteristico, uno a uno con los coeficientes de un polinomio típico de segundo orden: \(2\zeta\omega_n=\frac{R_a+K_{p1}}{La}\) y \(\omega_n^2=\frac{K_{i1}}{L_a}\).
De estas ecuaciones, podemos despejar \(K_{p1}\) y \(K_{i1}\) en función de los parámetros deseados \(\zeta\), \(\omega_n\), y \(t_s\):
- \(t_s=\frac{4}{\zeta \omega_n}\)
- \(K_{p1}=2\zeta\omega_nL_a−R_a\)
- \(K_{i1}=\omega_n^2_La\)
Tarea del Factor de Amortiguamiento (ζ): Para el lazo de corriente, el objetivo es una respuesta rápida con un sobrepico mínimo para evitar sobrecorrientes. Un valor ideal de ζ suele ser entre 0.7 y 1, lo que produce una respuesta críticamente amortiguada o ligeramente subamortiguada. Un valor de \( \zeta = \frac{1}{\sqrt{2}}\approx 0.707 \) es un compromiso excelente que produce una respuesta rápida con un sobrepico de solo 4.3%.
Lazo de Control Exterior: Dinámica de Velocidad
Siguiendo los mismo pasos descritos anteriormente, se procede a encontrár el polinomio caracteristico de la dinámica mecánica, es decir, de la velocidad.
Dinámica mecánica:
G_{mecánico}(s)=\frac{\omega_n(s)}{T_m(s)}=\frac{\omega_n(s)}{K\Phi I_a(s)}=\frac{1}{Js+K_{rot}} = \frac{1/K_{rot}}{(J/K_{rot})s+1}
La anterior es una función de transferencia de primer orden con constante de tiempo \(J/K_{rot}\). Recordar que se debe establecer el par de carga en \(T_L= 0\).
Controlador:
C_2(s)=(K_{p2}+\frac{K_{i2}}{s})=\frac{K_{p2}s+K_{i2}}{s}Asumiendo que el lazo de corriente es lo suficientemente rápido se tendría qué:
\frac{\omega_n(s)}{\omega_{ref}(s)}=\frac{K_{p2}s+K_{i2}}{Js^2+(K_{rot}+K_{p2})s+K_{i2}}El polinomio característico de este lazo es el denominador de la función de transferencia:
s^2+\frac{K_{rot}+K_{p2}}{J}s+\frac{K_{i2}}{J}Igualando los coeficientes con el polinomio canonico, se obtiene:
- \(K_{p2}=2\zeta\omega_nJ−K_{rot}\)
- \(K_{i2}=\omega_n^2J\)
- \(t_s=\frac{4}{\zeta \omega_n}\)
Tarea del Factor de Amortiguamiento (ζ): Para el lazo de velocidad, el factor de amortiguamiento se elige para obtener la respuesta dinámica deseada en la velocidad. Generalmente, se busca un valor entre 0.7 y 0.9, lo cual produce una respuesta rápida y sin oscilaciones excesivas (evitando el sobrepico en la velocidad)
A continuación encontrará un Script para matlab, el cual le permitirá simular de manera gráfica el comportamiento de las dinámicas de un controlador en cascada con en un motor de DC. Los parámetros del motor que se usa, se muestran en la interfase gráfica. Puede modificar el script con otros parámetros de motores y simular con ellos. Cambiar la extensión .txt por .m y ejecutarlo como script desde la ventana inicial de matlab.
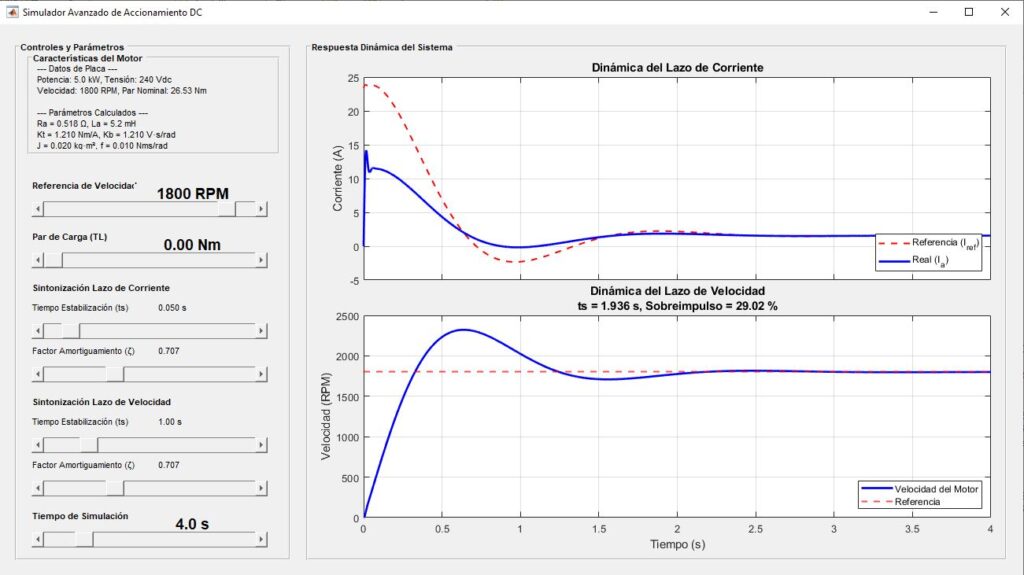
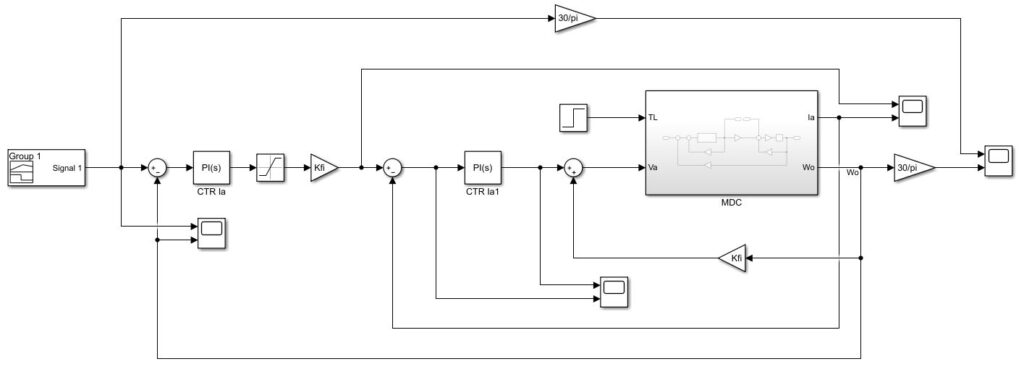
Se adicionan dos ficheros más, para ejecutar en Matlab Vr R2020a:
Se deben cambiar las extensiones de los archivos: En el archivo «CalculoVariables.txt», modificar la extensión a «.m», aquí estan las variables usadas en la simulación. En el archivo «MDC_02_2020a.txt», cambiar la extensión a «.slx», este es el archivo en simulink, descargar el fichero comprimido «Ejemplo_MDC.zip».
CONCLUYENDO:
En resumen, la combinación de la dinámica de primer orden del motor con un controlador PI siempre resulta en un sistema de segundo orden en lazo cerrado, cuya sintonización se realiza forzando al polinomio característico a coincidir con la forma canónica, permitiendo ajustar los parámetros del controlador \( K_p, K_i \) en función de la respuesta deseada \(\zeta, \omega_n \).